Naming the Notes
To write music, or play music, or to make any sense of it at all, we need to identify a difference between the notes, we have to be able to tell them apart. We need a name for each and every note. Not really a huge task because in Western music, there are only 12 notes. Shouldn’t be too hard to remember!
So, there are only 12 notes and we know that each one is a half step away (or a half tone away) from the next one. We also know that the frets on our mandolin are a half step apart. After you use up all 12 notes, they start over again – the notes start repeating. So, no matter what note you start on, 12 half tones higher is the same note. That distance of 12 half tones (12 semitones or half steps) is called an “octave”.
The same note repeated 12 semitones higher is said to be an “octave” higher than the original note.
The Natural Notes
So let’s see how it works. In music theory, we use the first seven letters of the English alphabet to name each of the 12 notes. Some notes might be sharp (eg. A#), and some may be flat (eg. Bb). Natural notes are notes without any sharps or flats. , There are seven of them, so the natural notes are A B C D E F G.
Here are the natural notes (starting with “A”):

The blank notes you see between the natural notes are sharps and flats. We’ll discuss them afterwards.
Some of the natural notes in the diagram above are separated by 2 half tones. They have another note in between them, which we’ll name later. But, some are only separated by a single half tone. It’s not a mistake.
There is only a half tone (or half step) between the notes B and C, and there is only a half tone between E and F. So there is no note in between. All the other natural notes are separated by a whole tone (2 half tones) and have a sharp or a flat note in between them. You may want to remember this, and I’ll probably mention it several times.
There is only a single half-tone (one step) between B and C, and a single half tone between E and F.
Where to begin
We know the separation between the natural notes, but we need one more thing to figure out which note is which – a starting point.
In diagram 5, we started with an “A note”. However, what if that first dot was an “E note”? Of course, we could still figure out all the other notes in the diagram because we know how many half tones there are between each natural note. We also know that they are arranged alphabetically. As a matter of fact, we could put any letter in any one of those dots, and figure out the rest of the notes. Why? Because we know the intervals (number of half tones) that separate each named note!
You’ll also notice in diagram 5 that the notes start repeating themselves after 12 half steps (12 half tones). The second A is obviously higher than the first. In fact, it’s 12 half tones, or an octave higher than the first A.
How does this look on our mandolin?
With what we now know, we can figure out all the natural notes on our mandolin. Let’s take a look!
First, we need our starting point, and we get that by knowing how our instrument is tuned. That tells us what pitch, or note each course of strings is tuned to .
The 4th string is G.
On our mandolin, the 4th string (the thickest course of strings) is tuned to the note “G” (the G just below middle C on a piano).
The 3rd string is D.
The next set of strings (the 3rd course) is tuned to “D”.
The 2nd string is A.
The second string (2nd course) is tuned to “A”.
The first string is E.
The first course of strings (the thinnest set) are tuned to “E”.
Take a look at Diagram 6. We’ve got the same notes that we saw in Diagram 5, only now we see them on the 4th string (G-string) of the mandolin. Notice that the note “A” starts on the second fret. The open string is G, so the A is two half tones up.
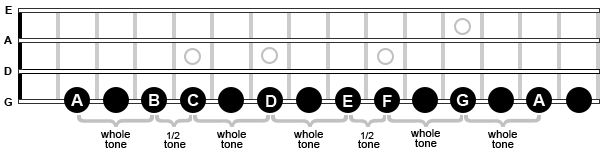
On your mandolin, the first course of strings is tuned to an E note. The second string is A. The third course is tuned to D, and the 4th string is G. This is shown on the left of diagram 6.
The distance between two notes is called an interval. For example, the distance between B and C is an interval of a semitone (or half tone). The distance between C and D is an interval of 2 semitones. The distance from C to E is an interval of 4 semitones, etc.
Now let’s look at the sharps and flats.